thesis : shape : experiment

3 flutes with the same clay, same volume and different shape

Based on the dimensions of the calculations, I made the 3 flutes. And the frequencies are almost the calculated frequencies! Except the one from the cube, as expected. Measurements were made directly after making the flutes, when the clay was still wet.

Playing while looking at a sound analyzer (Spectroid) allowed me to directly observe the fundamental frequency and its overtones something I had never seen before.

sphere-flute

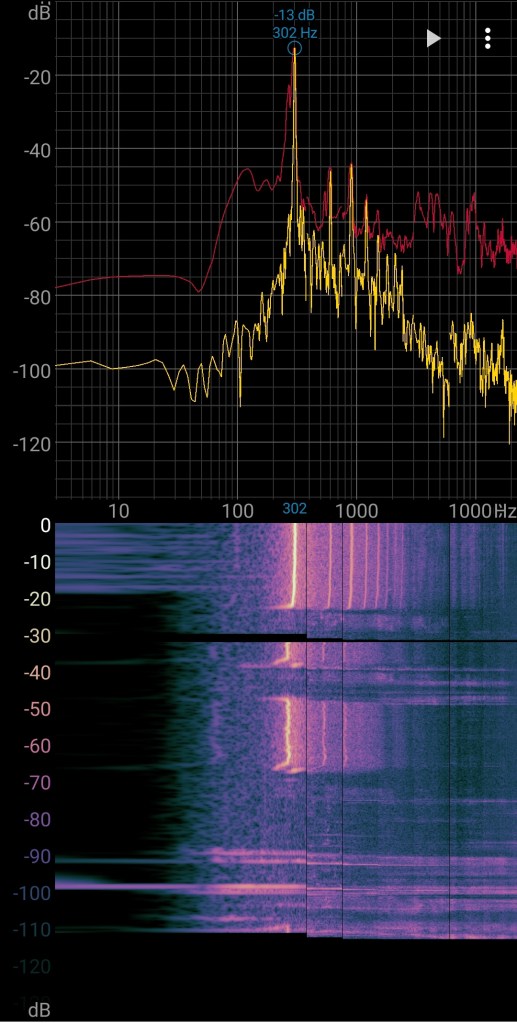
At the right side you can see the Spectroid with a clear fundamental of 302Hz and the overtones above. You can see how the overtones become closer and closer to each other, what looks like a logarithmic pattern.

In the next table you can find some measurements directly after making the flutes. When I research my flutes I always make multiple measurements with blowing more or blowing less into the flute. When you blow harder the pitch and amplitude increase. When you blow less the pitch and amplitude decrease. (The Amplitude scale: how louder how closer to 0)

Amount of blowing	Amplitude	Frequency
Little	-27dB	264Hz
Little	-22dB	252Hz
Much	-14dB	313Hz
Much	-13dB	302Hz

cube-flute

Amount of blowing	Amplitude	Frequency
Little	-31dB	246Hz
Little	-29dB	246Hz
Half	-26dB	264Hz
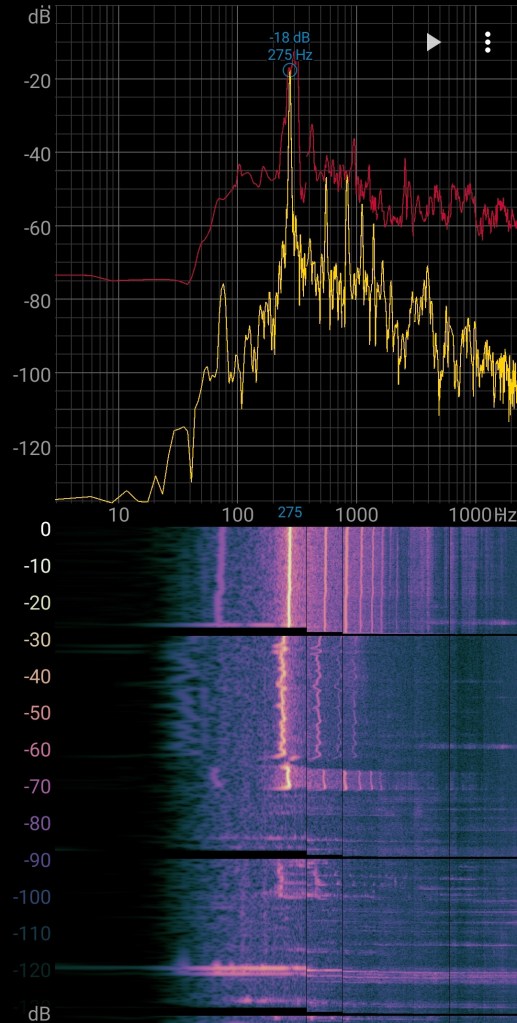
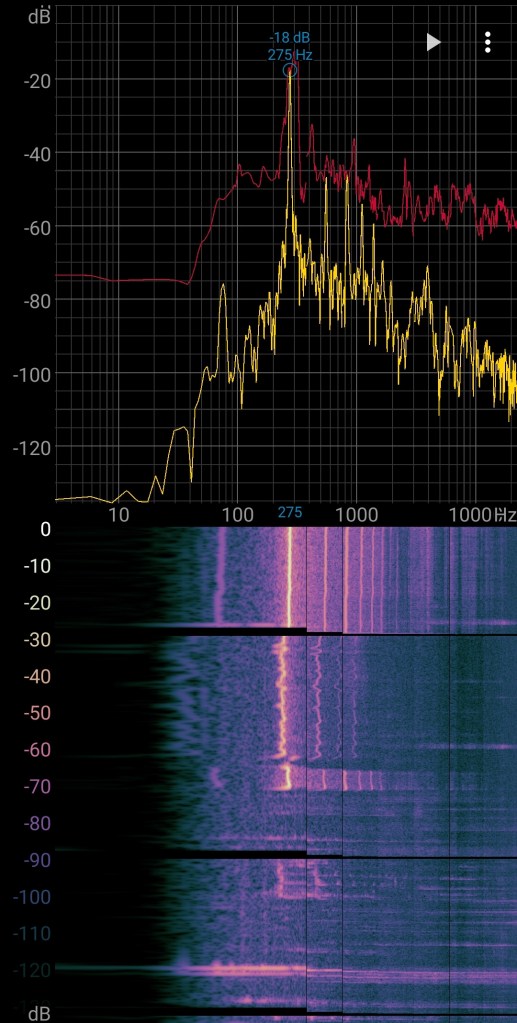
Much	-18dB	275Hz

The pitch is a bit lower than the pitch of the sphere flute.

sphere-flute vs cube-flute

Looking at the spectrogram of the sphere-flute and cube-flute you see that the relation between the overtones is (almost) the same. They have both 7 clear overtones which look like harmonic overtones

tube-flute

From now on, when I write about harmonics I refer to the overtones that look to be following a logarithmic pattern, and when I write about overtones I refer only to the non-harmonic overtones.

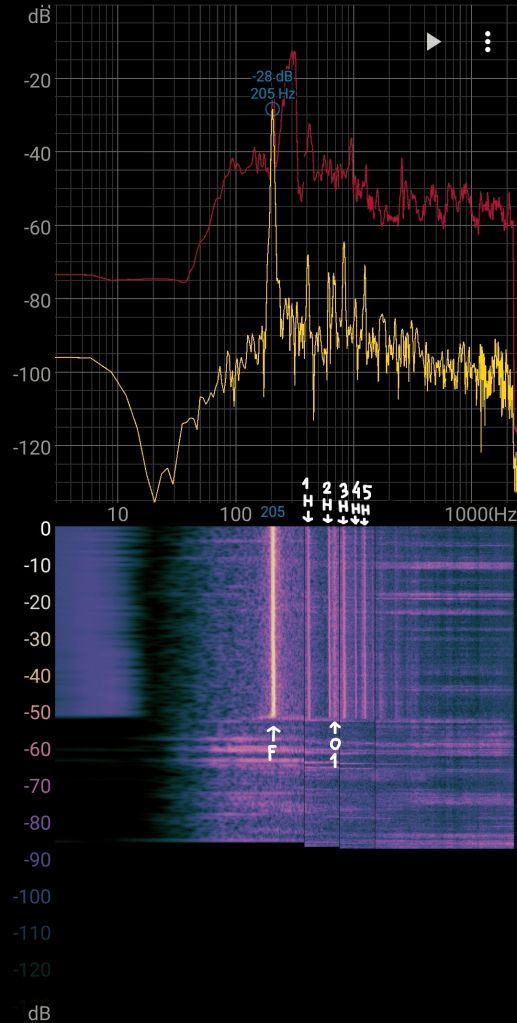
In the Spectroid you can clearly see the fundamental frequency (F) of 205Hz. Also, you can see the harmonic (H) pattern, but this time there is an overtone (O) between the 2^nd and the 3^rd harmonic. Moreover, when you blow harder into the flute it jumps (J) to that specific overtone.

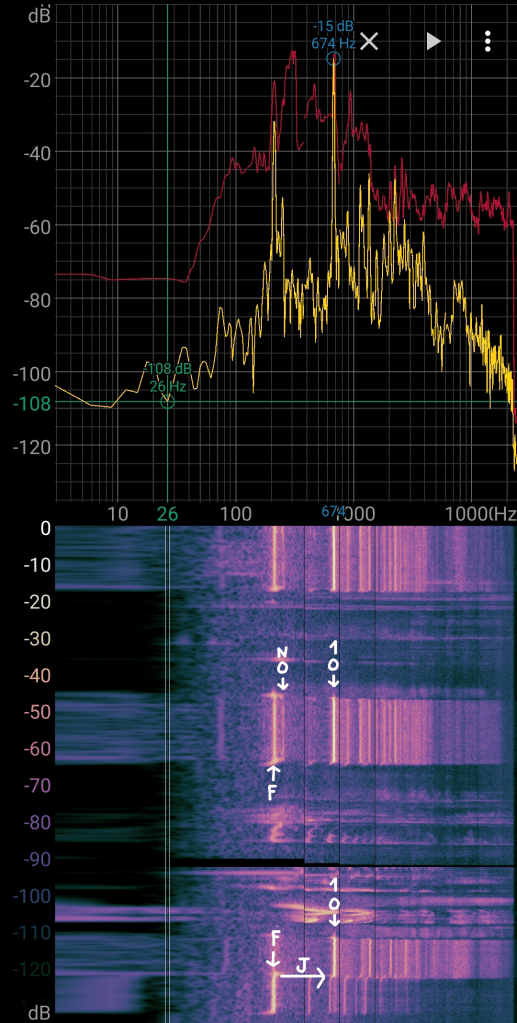
In the 1rst overtone (1O) picture you see below the jumping (J) moment from the fundamental to the 1rst overtone. Also, when sounding the 1rst overtone, the fundamental still sounds (but softer) and I also see a new overtone (NO) next to the fundamental.

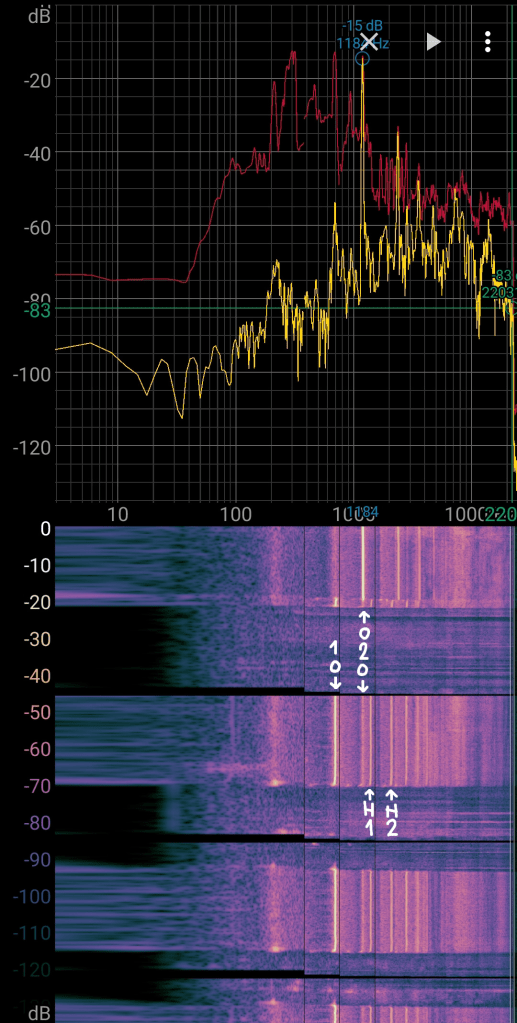
Playing the 1rst overtone, a new pattern appears above with harmonics and overtones. When you blow even harder you jump to the 2^nd overtone (2O), being the one between the 1rst overtone and the 1rst harmonic.

Many things are happening that I don’t understand yet: what makes that certain overtones and harmonics appear? Why can you overblow a tube flute? What I do know is that conventional instruments are made with certain specific dimensions (diameter and length) to only have harmonic overtones and when being overblown they jump to one of the harmonics. We are just seeing the ‘imperfections’ of my homemade flutes.

Amount of blowing	Amplitude	Frequency
Little	-22dB	211Hz
Little	-22dB	209Hz
Much	-40dB	199Hz

1rst overtone
	-15 dB	674 Hz
	-15 dB	697 Hz
2^nd overtone
	-15 dB	1184 Hz
	-15 dB	1194 Hz

sphere, cube vs tube-flute

When you compare the spectrograms of the sphere, cube and tube you see that the sphere and the cube have a much clearer logarithmic pattern with their overtones than the tube. The tube also has this clear harmonic pattern but with some added overtones.

A question I have had for a long time is: why isn’t it possible to overblow an ocarina? Why does it not have overtones? The second question is not correct, sphere flutes do have soft overtones above the fundamental, but we can’t play them. If you play a ‘tube’ flute you can easily jump from the fundamental frequency to the first or second overtone by blowing more or less into the flute. But with ocarinas this is not possible. What is then the turning point? If you stretch a cube at some point it becomes a tube, so why can you overblow tubes and not cubes?

Here a video where you can hear me playing the instruments and seeing live the sound analyzer:

How do sound waves move inside a sphere?

Trying to understand how the waves move inside an ocarina I did a little test with water:

In an ocarina the air enters from one side of the sphere, so I decided to let the drops of water fall next to the borders, to let the waves start from there.

In this drawing you see how the waves move from the right side to the left side (drawing 1), then they bounce with the borders creating two points (drawing 2) where the waves move towards and these two create one point (drawing 3). This is 2 dimensional, while inside of an ocarina the waves move in 3 dimensions. But in some way, it’s a little glimpse of how the waves interact inside a sphere creating complex interference patterns. I guess the spherical shape makes one frequency resonate (constructive interference) and the rest ‘disappears’ because of destructive interference. This is something I will further research after graduating.

shape : invitation