thesis : shape : theory

In this chapter I will compare inner spaces made with the same material, same volume, but differing in shape by making 3 flutes: a sphere, a cube and a tube.

The sound wave produced by flutes comes close to a sine wave because it has a strong fundamental frequency, and the overtones sound softly. That’s why we perceive it as a very pure tone.

Also, I chose to make flutes because I have experience making and researching them. While making them you can directly play them and tune them. This makes it possible to directly measure their pitch and amplitude, although the pitch and amplitude will change because of a shrinkage produced by the drying and firing process.

You can find here the calculations I made to make 3 flutes with the same clay, same volume and a different shape.

reference-flute

The most recent flute that I have made is the sphere-flute of 55Hz. I used this flute as reference to check if my way of calculating the volume and frequency is correct for a sphere flute.

To calculate the frequency, I used the formula from the Helmhotz Resonators.³²

The flute of 40cm diameter (radius = 20cm) with an opening for the flute mouth piece of radius 1,5cm and length 2 cm has a frequency of around 56,06 Hz.

d = diameter
r = radius
ro = radius opening mouth piece
lo = length opening mouth piece
V = volume
Ao = Area opening mouth piece
F = frequency

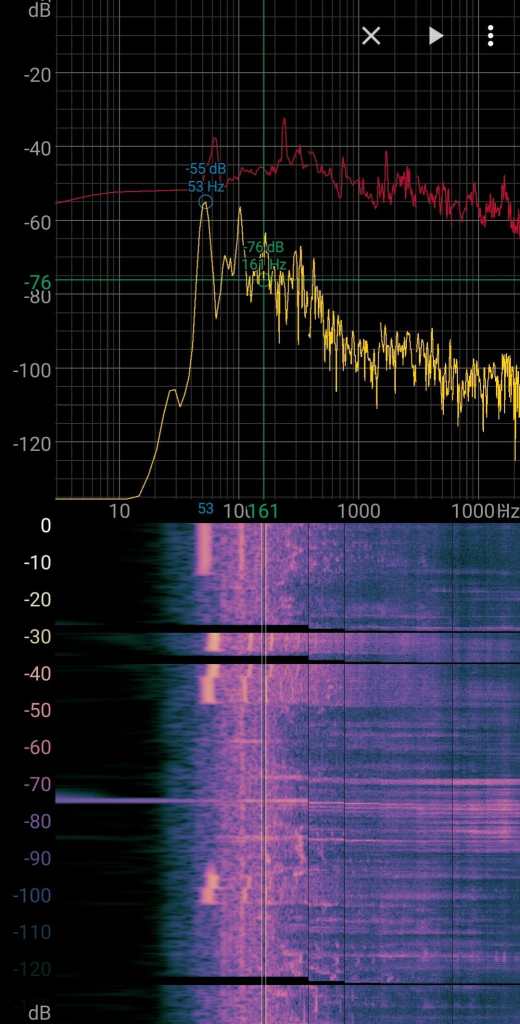
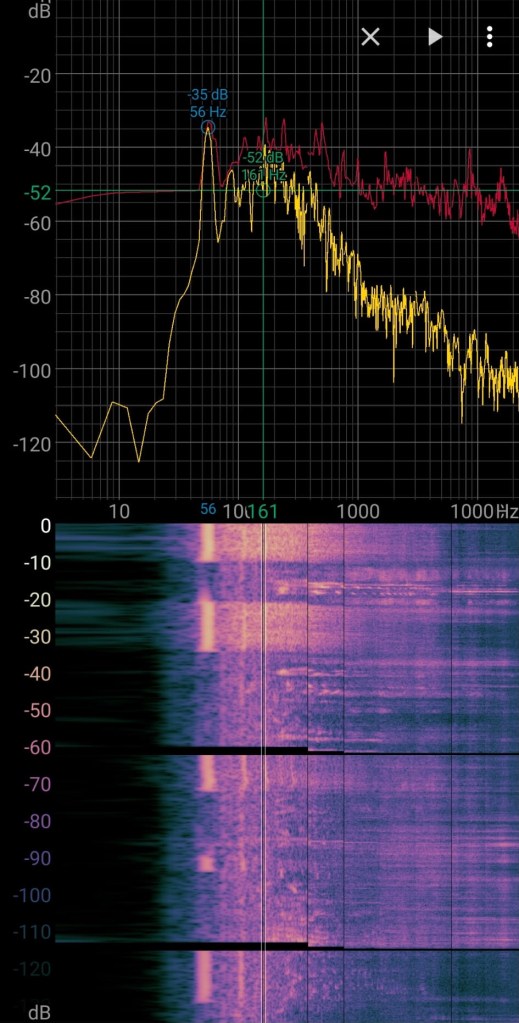
For amplitude and frequency measurements I have been using different apps. This was the first time I used the Spectroid App. Above you see in blue the pitch in Hz and the amplitude in dB of the fundamental frequency. In the left picture 53Hz and in the right picture 56Hz, so the calculations work! Also, you can see some overtones!

32. Listening to a Helmholtz Resonator you hear the same tone as playing it like a flute. And vice versa.

3 different shapes with same volume

sphere-flute

I started calculating the sphere-flute. I chose a handy size: not too big and not too small: 6cm diameter
Based on a diameter of 6cm I calculated the volume = 268,98cm3
This will be the volume also for the cube and the tube flute.
I estimated the radius of the opening mouth piece to be 0,5cm and the length of the opening mouth piece 1cm.
With this I could calculate the frequency:

cube-flute:

Starting with a volume of 267,08cm3 I calculated the dimensions of the cube. Being the length of the sides = d
Using the formula f= v/(2*d), which is normally used to calculate the resonating fundamental frequency of a room, I calculated the frequency of 2658,9Hz, very high comparing it with the 295,45 Hz of the sphere flute. I expected it to have more or less the same pitch as the sphere flute…

tube-flute:

Keeping the volume constant (267,08cm3) with a smaller radius the tube becomes longer and if I make the radius bigger the tube becomes shorter. I know from making other flutes and my bachelor thesis that the thinner the tube the easier it is to make a flute sound, but, on the contrary, the shorter you make a tube the easier it is to make the shape. I decided to make the radius (r) of the tube 1,6 cm to get a reasonable length of the tube (h) (22,42cm).

With this numbers we can calculate the fundamental frequency.³³ I calculated the frequency of the tube with a closed end and an open one.^{34, 35}

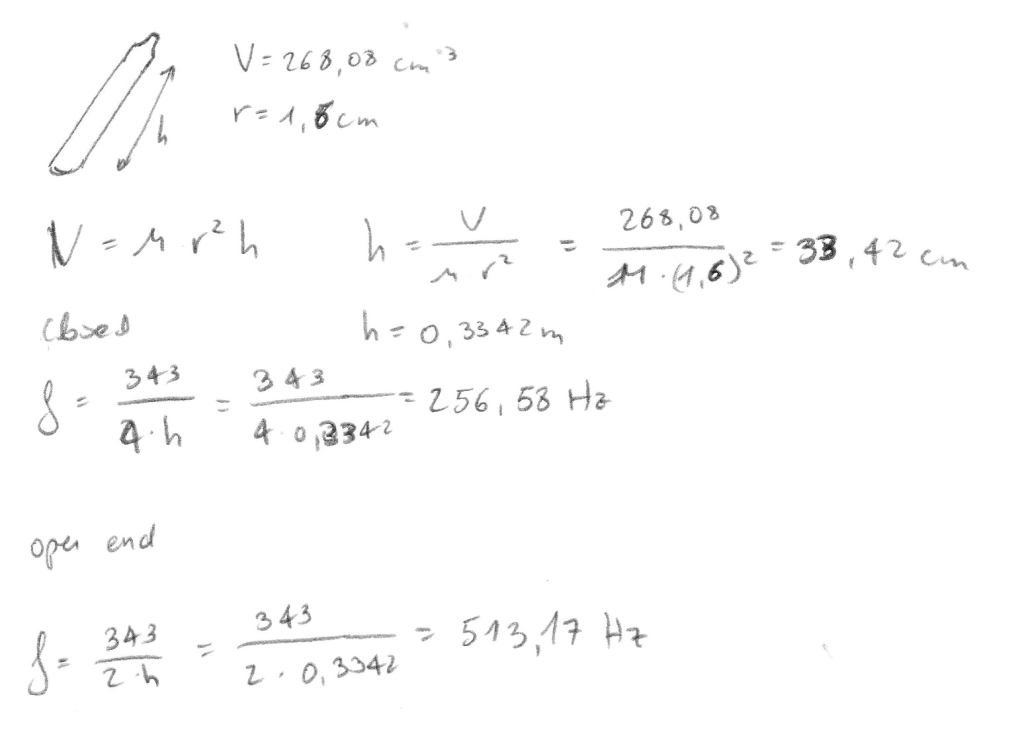
Later I realized that I did not calculate the opening for the mouthpiece for the cube flute and the tube flute. When you make extra holes in the flute to make extra tones, the holes make the flute sound higher. I suppose that taking this into account, the results of the calculations would have been higher frequencies.

33. Formula physically checked with other tube flutes.
34. M. Breinig “Standing Sound Waves”, tubes with two open ends and tubes with one open and one closed.
35. Tom Henderson “Sound Waves and Music”, Lesson 5 Physics of Musical Instruments, Open-end air columns and closed-end air columns.

shape : experiment